Nel caso reale, i contorni saranno in qualche sfumati; esisterà, cioè, una zona grigia più o meno ampia in corrispondenza di ogni transizione.
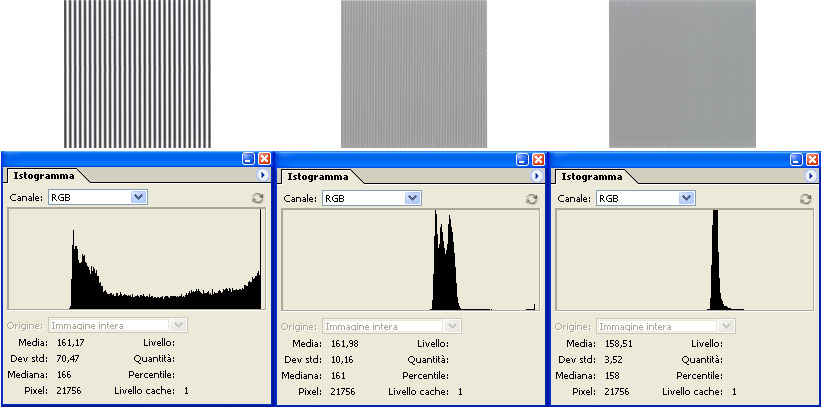
Tre esempi di target di frequenza spaziale crescente. L’istogramma mostra come, all’aumentare della frequenza spaziale, la differenza tra il livello massimo Lmax e quello minimo Lmin dell’immagine si riduca progressivamente.
Si immagini ora di fotografare diverse serie di linee sempre più ravvicinate tra loro, cioè di frequenza spaziale crescente. Si arriverà, presto o tardi a seconda della bontà del sistema in prova, al punto in cui le zone grigie in corrispondenza delle transizioni bianco/nero risulteranno parzialmente sovrapposte. In questa condizione, i livelli di grigio non raggiungeranno più i valori 0 (nero) e 255 (bianco), ma oscilleranno tra due valori intermedi. Questo equivale a dire che il contrasto, definito appunto come rapporto tra livello di bianco e di nero di un’immagine, è diminuito.
Proprio su questa considerazione si basano le prove di risoluzione condotte dalla maggior parte delle riviste di settore e dei laboratori di misura. La misura del potere risolutivo di un oggetto viene cioè ricondotta a una misura di contrasto dell’immagine prodotta.
È possibile definire allo scopo un valore di contrasto per la zona n-esima: (C)n = (Lmax-Lmin)n / (Lmax-Lmin)ref
Dove L rappresenta di livelli di grigio all'interno dell'immagine e "ref" indica semplicemente una zona di riferimento, cioè una zona di frequenza spaziale abbastanza bassa da assicurare la completa separazione bianco/nero.
La funzione così definita ha un valore massimo pari a 1 (viene infatti divisa per la differenza di livelli maggiore presente nell’immagine) e un valore minimo teorico pari a 0, che raggiungerebbe qualora la zona fotografata fosse di colore uniforme.
Rappresentando in grafico (C)n in funzione della frequenza spaziale dei target fotografati, si ottiene una curva che parte da 1 (o dal 100%, se si preferisce) e decresce più o meno linearmente fino a tendere a 0.
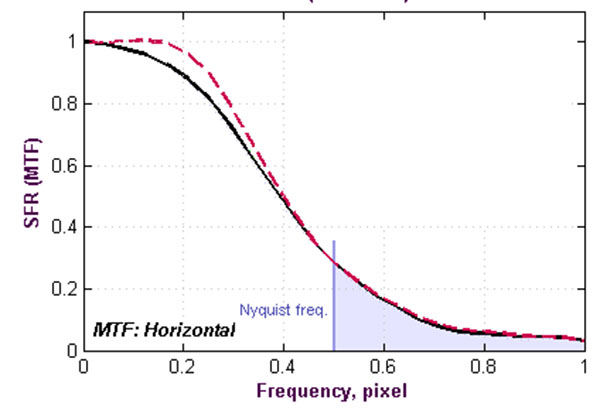
Un esempio di curva MTF, espressa in funzione di cicli per pixel. 0,5 cicli/pixel è, per cosiddetto "teorema del campionamento", il massimo valore misurabile.
Un simile grafico è tutto ciò che occorre per valutare in modo oggettivo il potere risolutivo di un oggetto in prova: basta infatti scegliere arbitrariamente un opportuno valore di caduta di contrasto, ad esempio pari al 50%, e leggere sul grafico il valore di frequenza spaziale corrispondente - maggiore è il valore di frequenza spaziale, migliore la risoluzione. Poco importa che tale grafico venga ottenuto in pratica con un procedimento manuale riconducibile a quello appena descritto (che per inciso, è rappresentativo di una metodologia realmente utilizzata, anche se obsoleta) oppure con metodi più analitici, che coinvolgono derivate e trasformate di Fourier.
Tali grafici prendono il nome di "MTF" (Modulated Transfer Function), essendo di fatto rappresentazioni di funzioni di trasferimento (cioè relazioni tra l'ingresso - l'immagine da fotografare - e l'uscita - l'immagine creata - del sistema fotocamera) "modulate", cioè attenuate. Nulla di esoterico, si tratta solo di gergo.